ポアソン方程式　56倍の高速化

ポアソン方程式 Uxx + Uyy = r を解くひとつの方法は、フーリエ変換を使用する方法です。
この解法をCPU上で数値的に解くとき、フーリエ変換はFFTWのような高速フーリエ変換ライブラリを使用して
行われます。 我々のプログラムでは、GPUを使用してポアソン方程式を解きます。FFTはCUDA FFTを使用します。
CUDAカーネル上でフーリエ空間上の解を得ることができます。
例えば、2048×2048のメッシュサイズのとき、FFTのみでは174倍のスピードアップとなり、
CPU-GPU間のメモリー転送を含んだ合計でも56倍のスピードアップとなりました。
下のグラフは、いろいろなメッシュサイズの場合の比較結果です。

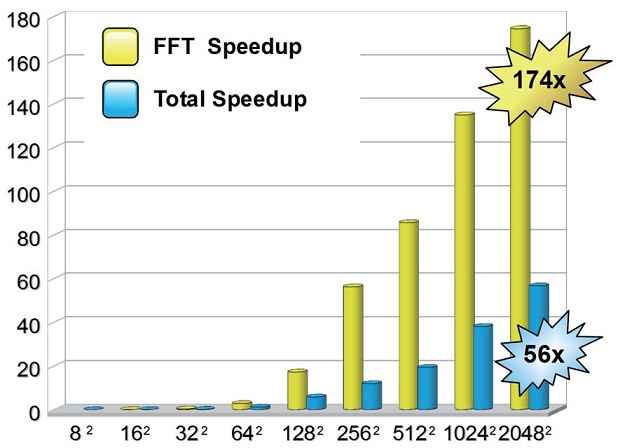
二次元ポアソン方程式をGPUで解いた場合の対CPU倍率です。
（CPU1コアで解いた場合の数値を１とした場合の倍率）
横軸はメッシュ数、縦軸は倍率です。