English 
日本語 
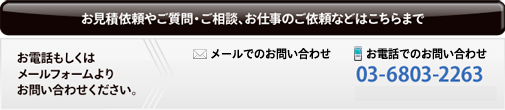
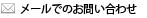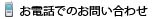Higher order elementsによる高精度な数値解析
IMPETUS Afea Solverは、線形要素だけでなく、最大で三次の高次精度Solid要素を扱うことが出来ます。
１つの線形六面体要素に対して、内部節点を合わせて合計64の節点を持つ要素です。
塑性変形に対してとても優れています。
- 通常Solid要素では扱えない板厚の薄いモデルでも高精度な解析を行うことが出来ます。
- 六面体要素だけでなく四面体要素でも高精度の解析を行うことが出来ます。
- 元のメッシュデータはそのままに、解析実行時に要素の次数を変更することが出来ます。
１つの線形六面体要素に対して、内部節点を合わせて合計64の節点を持つ要素です。
塑性変形に対してとても優れています。
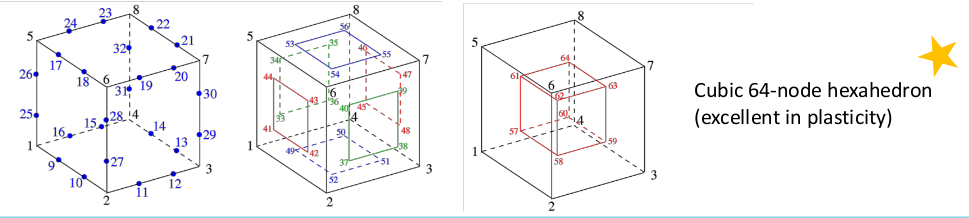
片持ち梁の曲げ解析１
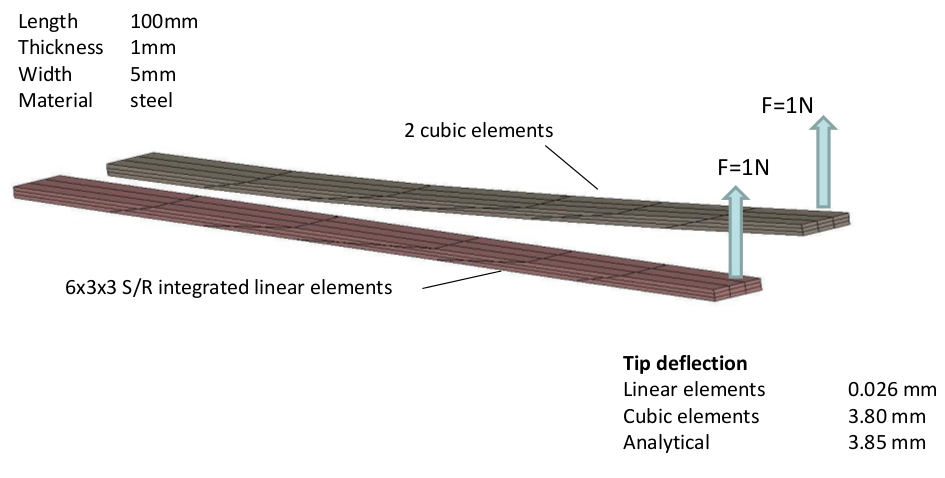
線形１次要素では6×3×3の要素数を使用しても、このような薄い要素の曲げを再現することができません。
cubic(三次)要素ではわずか2要素でも理論値に近い曲げを再現することが出来ます。
cubic(三次)要素ではわずか2要素でも理論値に近い曲げを再現することが出来ます。
片持ち梁の曲げ解析２
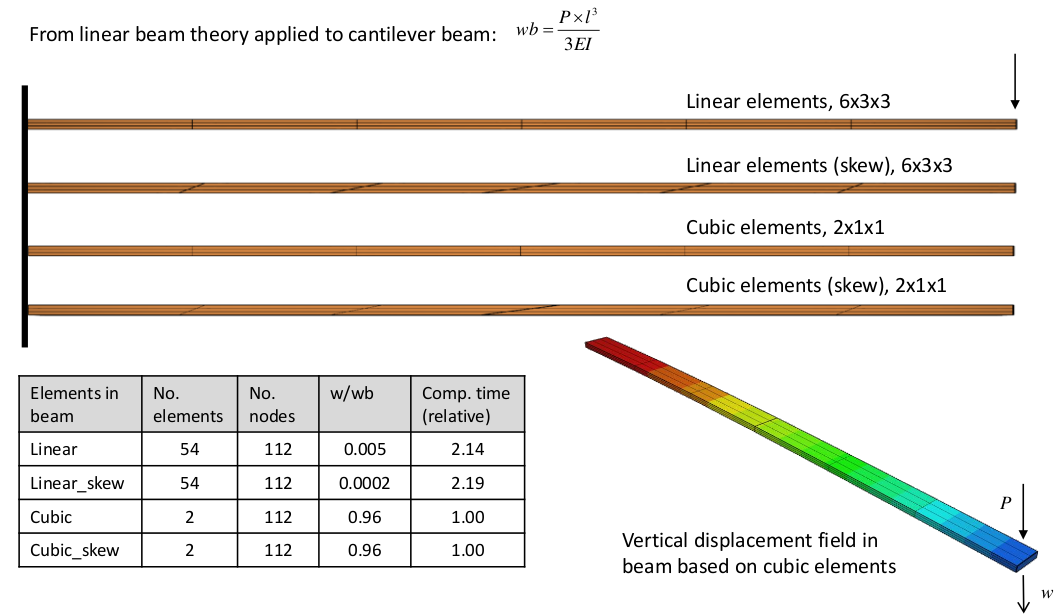
メッシュの歪みがあっても精度は落ちません。
計算時間は一次要素に比べて半分以下になっています。
高次精度要素
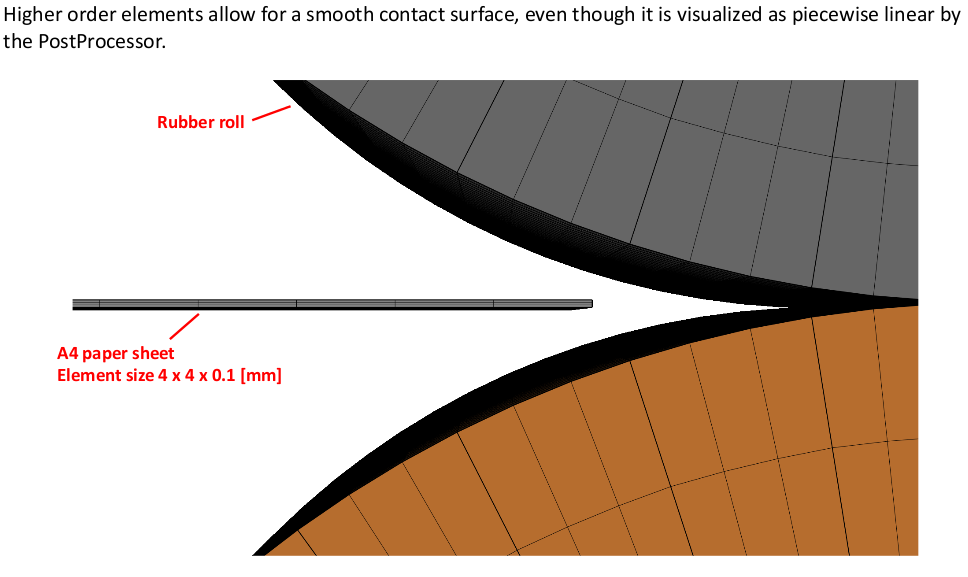
ペーパーローラーの解析
厚さ1mmの薄いA4ペーパーの巻き取りも高次精度Solid要素を使用することで、精度良く解析できます。
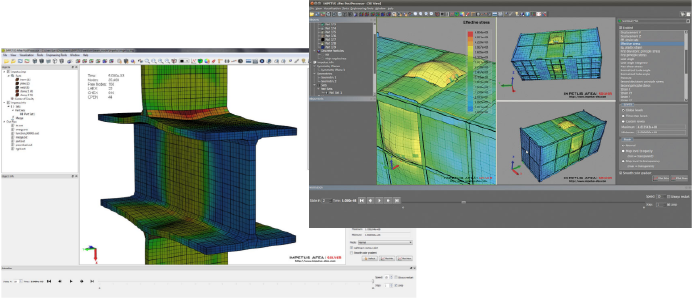
高機能ポストプロセッサー
IMPETUS Afea Solverは専用のポストプロセッサーを搭載しています。
高品質なグラフィックレンダリング機能に加え、コンタープロット、グラフ作成、テキストデータ編集、動画作成など
必要なポスト処理が簡単に行なえます。
高品質なグラフィックレンダリング機能に加え、コンタープロット、グラフ作成、テキストデータ編集、動画作成など
必要なポスト処理が簡単に行なえます。
